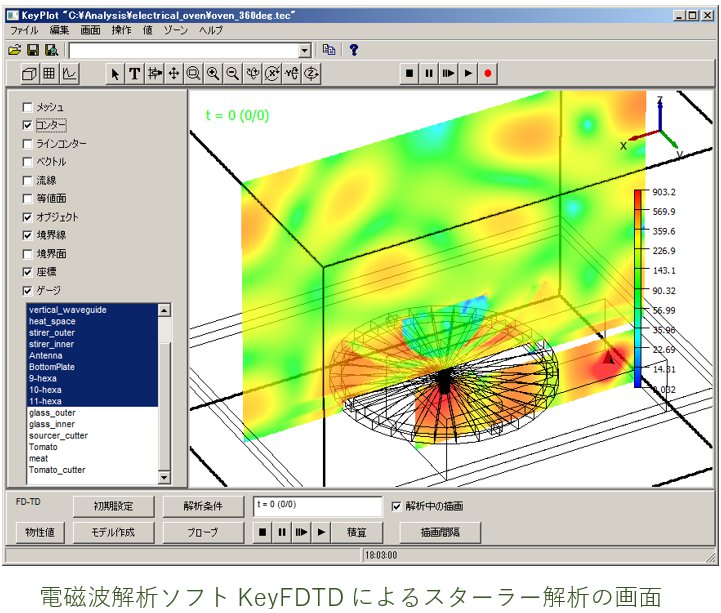
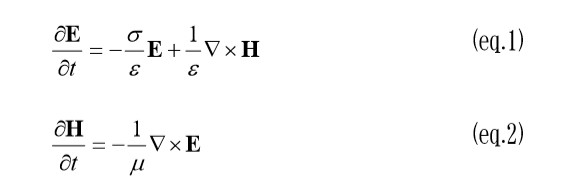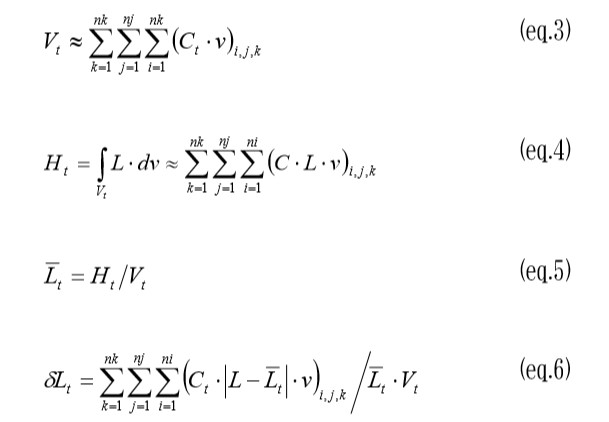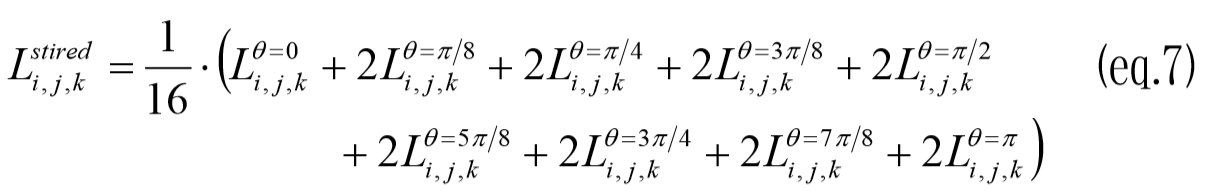電子レンジの加熱均一性評価

はじめに

電子レンジのようなマルチモードマイクロ波加熱器は極力均一な加熱量分布を実現するために様々な工夫がなされています。 その代表的なものが、スターラーによる内部電界分布を攪拌する方法です。 スターラーの形状や配置は実験を繰り返すことで加熱分布が均一に近くなるように設計されてきました。 しかし、実験には実物の作成が必要なことや、測定が難しいこと、定量化が困難なこと等、様々な問題があります。

そこで、「電磁波解析の巻２」前編では、FDTD法による電磁波解析を用いて電子レンジにおけるスターラーの均一加熱に対する効果を定量化する方法を構築し、取り上げたモデルにどの程度の効果があるかを示すことにします。 解析には弊社が開発・販売する電磁波解析ソフトKeyFDTDを用い、解析結果をファイルに出力してその値を集計することにより上記の定量化を行うことにします。

電子レンジは奥が深い

非常に身近な調理機器になった電子レンジですがその身近さ故に手抜き料理の代名詞に使われることもあります。 しかし、マイクロ波加熱器としての電子レンジは技術的に大変興味深いものであり、どのように設計すれば様々な料理を均一加熱できるかという問題がしばしば取り上げられます。 例えば、加熱庫内の形状やマイクロ波を攪拌するためのスターラーと呼ばれる部品の形状と動き、加熱出力について検討がなされています。 科学技術研究所でもこれらの点に興味を持って電磁波解析を行っています。

今回はスターラーに注目

スターラーは電子レンジの均一加熱に対してとても大きな役割を果たしています。 廉価な電子レンジは均一加熱のために、くるくると回るターンテーブルを採用していますが、ミドルエンド以上の機種になると必ずターンテーブルではなくスターラー型となります。 勿論これはターンテーブルがない分、掃除しやすいということが大きな理由ですが、スターラー型の方がターンテーブル型より加熱均一性も優れていることが一要素としてあるからです。

電磁波解析と加熱均一性評価

加熱均一性の評価については、かぎけんが数年来取り組んで来たテーマであり日本計算工学会等の論文でも発表しています。 本号では、この研究使った手法を用いて加熱均一性を評価し、スターラーがどの程度効果を発揮しているかを検証します。

FDTD 法について

FDTD法は支配方程式をMaxwell方程式とし、それを時間空間について離散化して、陽的に少しずつ時間を進めながらある時刻における電磁界を求める手法です。

ここで、それぞれの変数は表1の通りです。

表1: 変数表

変 数	物 理 量	単 位
t	時間	s
E	電界ベクトル	V/m
H	磁界ベクトル	A/m
ε	誘電率	F/m
μ	透磁率	H/m
σ	導電率	S/m

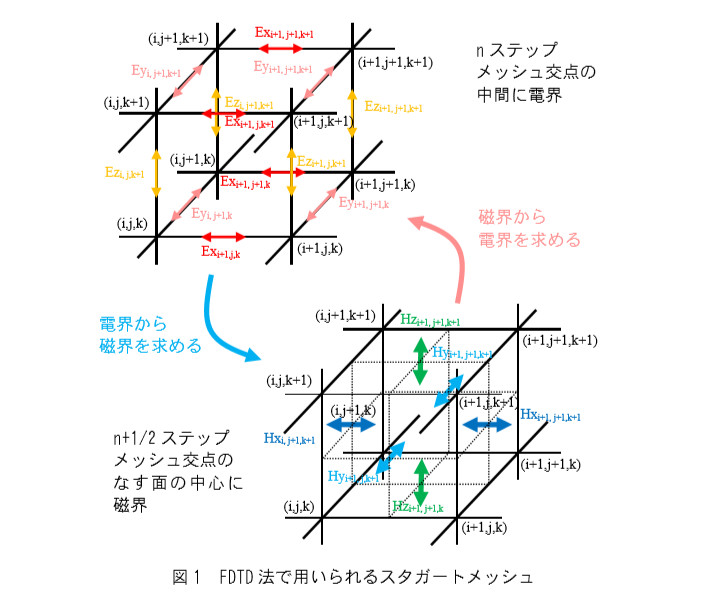
離散化は時間的・空間的にメッシュに対して物理量が半メッシュずつずれたスタガードメッシュ「(図1 FDTD苞で用いられるスタガートメッシュ」を用いて行ないます。 時間的に半メッシュ（半タイムステップ）ずらすことで解析に必要なメモリ容量が節約でき、空間的に半メッシュずらすことで (eq.1) 、 (eq.2) の回転（∇×）項の計算が効率的に行なえるというメリットがあります。

少々脱線しますが、．．．

スタガートメッシュは圧力の振動的な解を避けるために流体解析でも用いられます。 圧力をメッシュ交点、3 次元の速度成分 u, v, w をそれぞれ X, Y, Z 方向のメッシュ交点中点に配置し、図 1 の電界と類似しています。 また、メッシュの交点上に物理量を持つメッシュもしばしば数値解析では使用され、コロケーテッドメッシュと呼ばれ、熱流体や 構造解析など、幅広く用いられています。

加熱量と加熱ムラの定量化

FDTD解析で求められるのは電界ベクトルと磁界ベクトルでその２つから各点における損失（誘導損失＋誘電損失、つまり加熱量）が求められます。 加熱ムラはこの損失の分布について以下の式で標準偏差を導出しその大小で評価します。それぞれの変数を表2に示します。

表2: 変数表

変数	物理量
ni, nj, nk	解析領域のX,Y,Z方向メッシュ数
i, j,k	X,Y,Z 方向のメッシュ番号
Ct	加熱対象物内部に関する係数 1：（加熱対象物内部） 0：（それ以外）
ν	メッシュがなすコントロールボリュームの体積
Vt	解析で再現された加熱対象物の体積
L	局所損失
Ht	総加熱量
	平均加熱量
δLt	加熱量標準偏差

解析モデルと条件

図2にスターラーのある電子レンジでトマトの肉詰めを加熱する解析モデルの概略を示します。

科学技術研究書の創刊号ではモデル化が簡単な横から電磁波が入射する電子レンジを解析しましたが、今回はスターラーの影響を考慮するため下からスターラーをアンテナにして入射するモデルに変更しました。 この加熱庫内中心に直径24cmの深皿に肉詰めのトマト（直径: 8cm, 肉詰め径: 6cm）を乗せて加熱する解析を行いました。 なお、図2はスターラー（肌色の部分）が見えるように肉詰めトマトと皿の描画を半透明にしてあります。

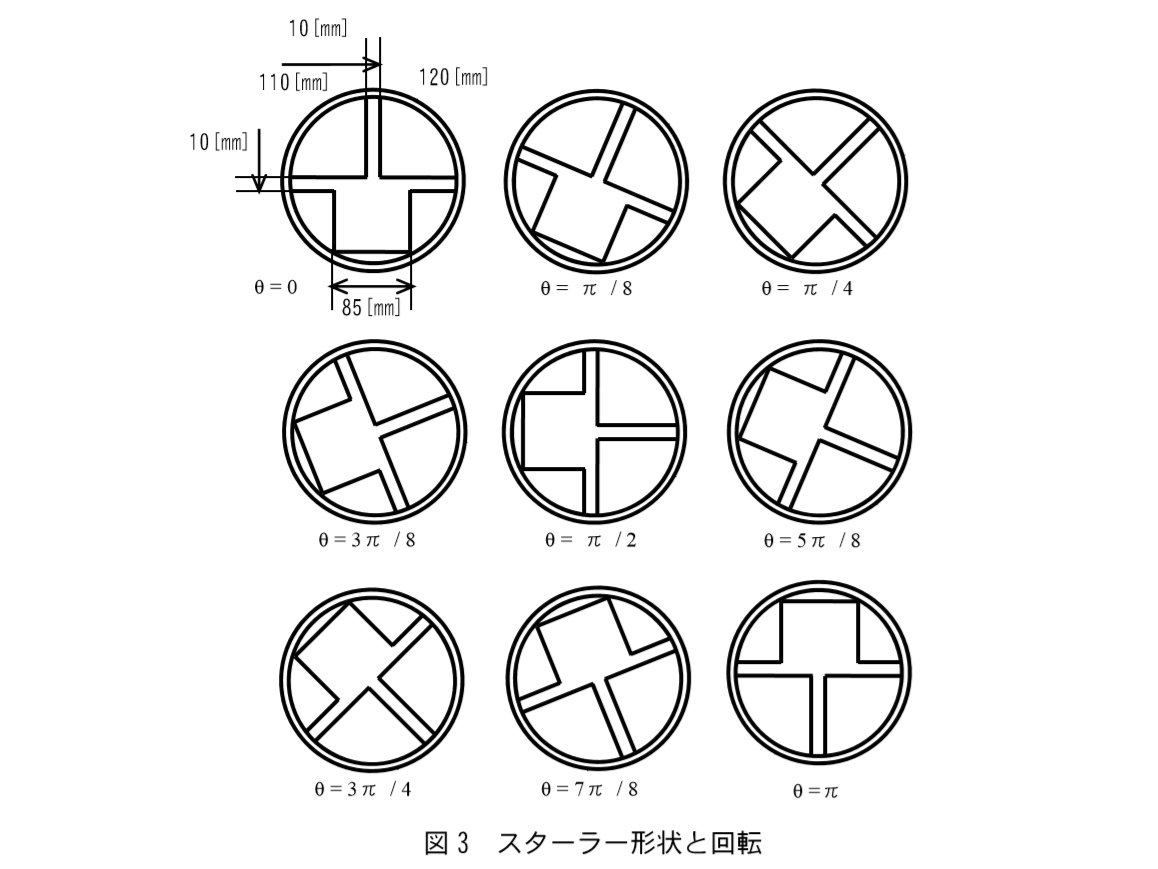
解析条件は、導波管の端部にマグネトロンの電極を模した点源を配置し周波数2.45GHzの正弦波で励振しました。 スターラーについては図3に形状を示します。 スターラーの回転は単独のFDTD解析でモデル化することが出来ないので回転を16分割した各回転角を想定したモデルを作成し、それぞれの解析結果の損失分布を平均することで回転の影響を解析しました。 但しπ/8～15π/8は対称なので(eq.7)を用いて9ケースの回転角について解析を行い1回転分の平均加熱量を求めました。

解析設定

9ケースについて等間隔 2mmで201×151×169（≒520M）メッシュを用いました。 電子レンジのように誘電率の分布がある解析対象に対しては不均一メッシュを用いてメッシュ数を減らし解析速度を向上させるのが一般的ですが、この問題で不均一メッシュを用いると収束性が極端に悪いことが確認されたので等、間隔メッシュを用いました。

表3に今回の解析で用いた物性値を示します。 電子レンジの加熱庫内の壁面や導波管の壁面は導電率∞の完全導体を仮定しました。 トマトやフィリング（肉詰め）は部位によって物性が異なると考えられます。 特にフィリングはタンパク質と脂質、水分の混合物なのでその傾向が強く、一般に脂質は低誘電率・高誘電損失であり、水分は高誘電率・中誘電損失なのでフィリングの中でも物性値は大きく異なります。 本来ならこれらも考慮すると大変興味深い結果が得られると考えられますが、今回の解析ではフィリング部分の物性は一定とし、内部における分布の考慮は今後の課題としました。 なお、かぎけんでは富士電波工機株式会社と協力して、現場で操作しやすい誘電率測定システムを開発しています。

表 3 解析に用いた誘電率

物質	比誘電率	tanδ（誘電正接）
空気	1	0
レンジ壁面	0	0
トマト	55	0.05
フィリング	28	0.2
皿	4	0.001
テフロン底板	2	0.0001

解析結果（電界強度）

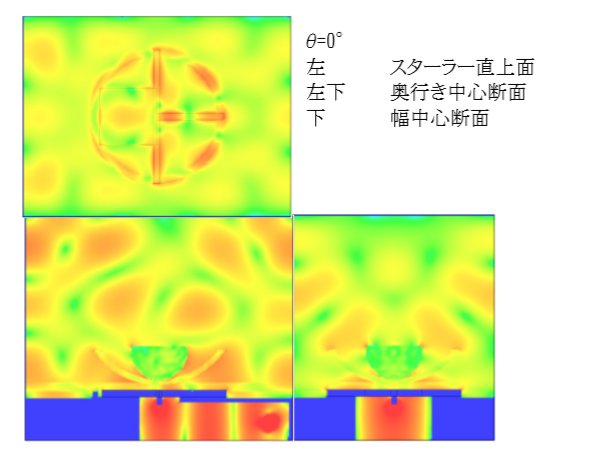
θ = 0°

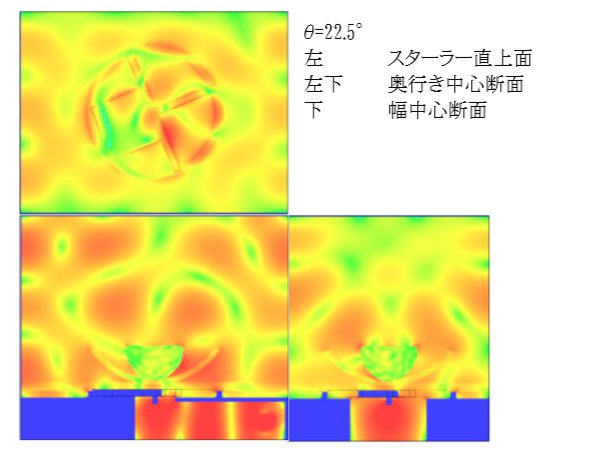
θ = 22.5°

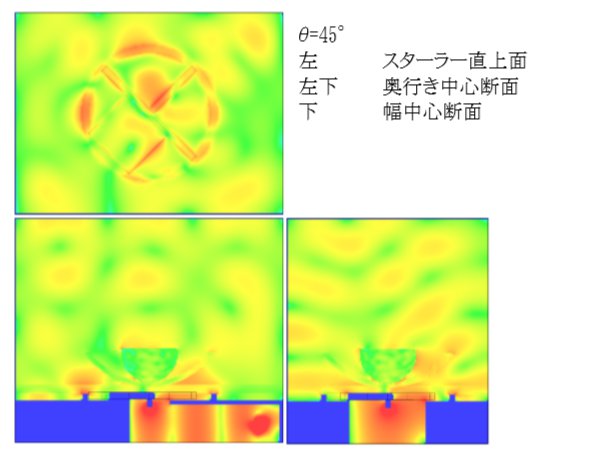
θ = 45°

θ = 67.5°

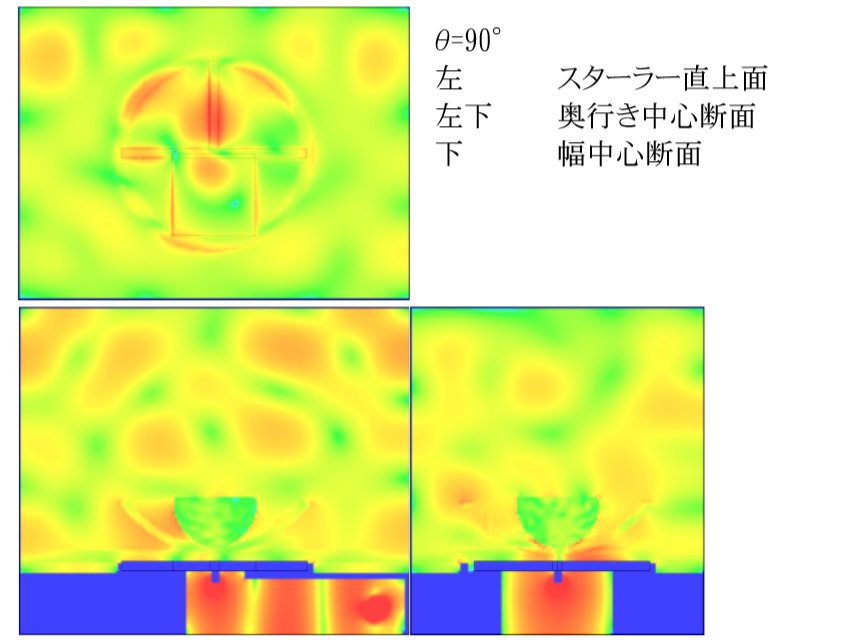
θ = 90°

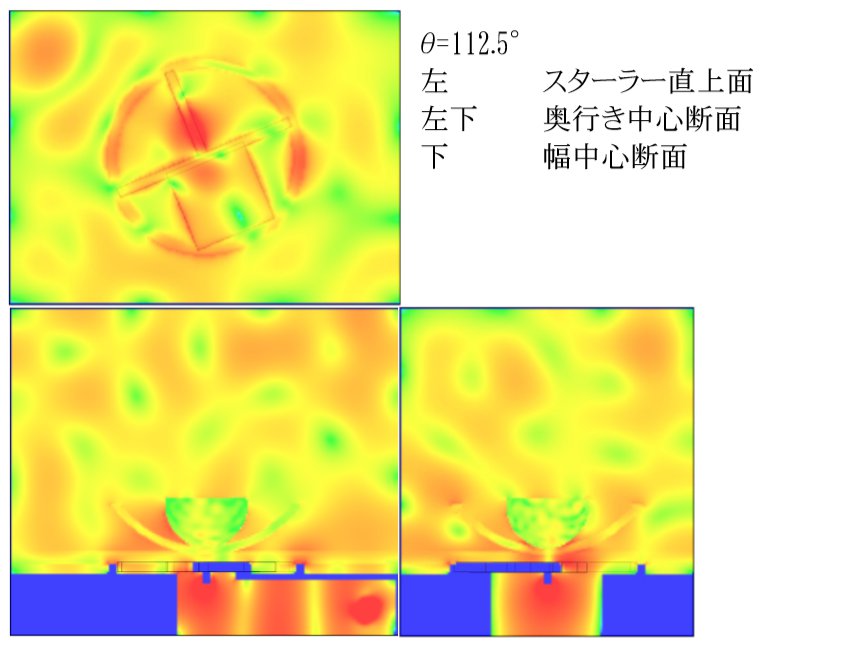
θ = 112.5°

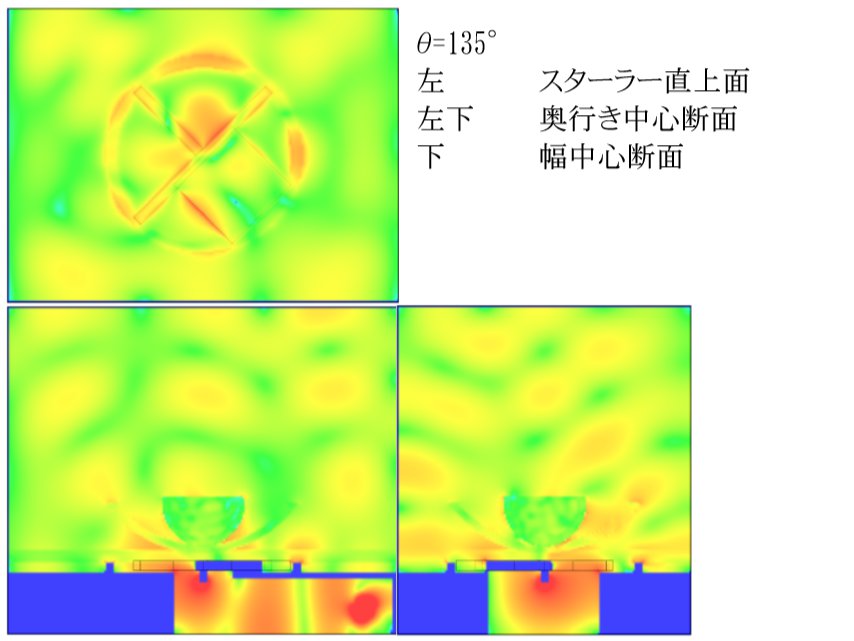
θ = 135°

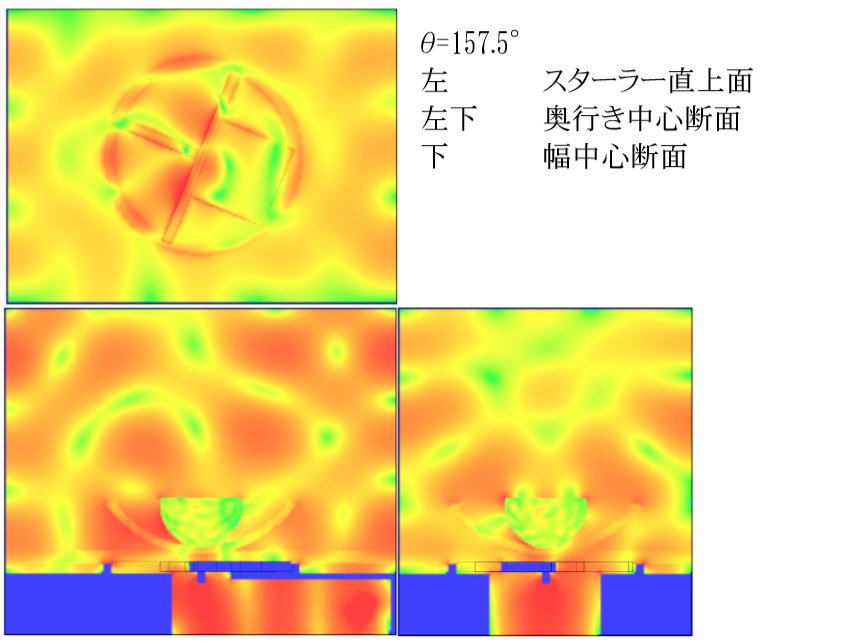
θ = 157.5°

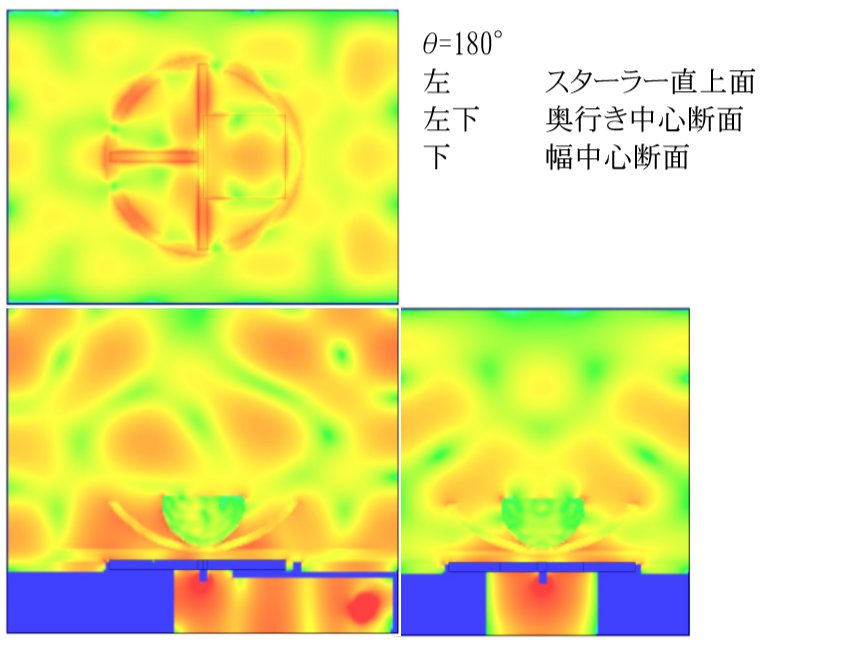
θ = 180°

備考

今回の解析モデルは奥行きに対して面対称となっているため「θ > 180°」の解析は「θ=202.5°⇔θ=157.5°、θ=225°⇔θ=135°、θ=247.5°⇔θ=112.5°、θ=270°⇔θ=90°、θ=292.5°⇔θ=67.5°、θ=315°⇔θ=45°、θ=337.5°⇔θ=22.5°」の組み合わせで鏡像対象となるため解析を行なう必要がなく、「θ < 180°」の結果を用いて値が得られます。 これにより解析結果から求められた無次元化加熱量と加熱量標準偏差は 180°を中心として対称になることに注意して下さい。

但し、この方法が使えるのは料理や皿も含めて加熱庫内部がスターラーの回転中心に対して軸対称の場合のみです。 加熱庫や導波管、スターラーの形状が鏡像対象の場合でも料理や皿が上記の条件を満たさない場合は 0°から 360°の解析を一通り全て実行する必要があります。

加熱均一性の定量的評価

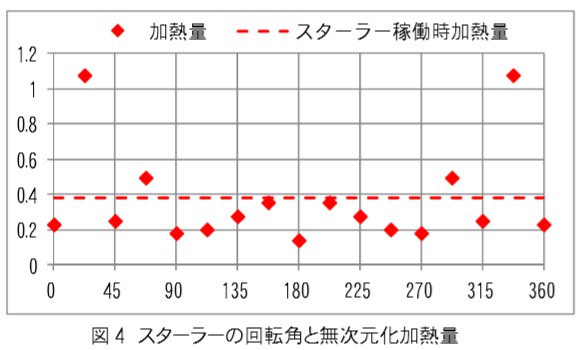
次にそれぞれのケースについて加熱量及び加熱均一性を評価した結果を示します。 加熱量は無次元化されており、標準偏差は無次元化された加熱量のトマトの肉詰め内部の標準偏差です。

解析結果について

この解析において無次元化加熱量は電子レンジの加熱効率とも言えます。 図4を見るとスターラー回転角22.5°、337.5°の場合に極端に加熱量が大きくなっています。 これはこの角度の場合に励振源から発振され導波管を通して加熱庫内に入るエネルギーが入りやすく、閉じ込められやすくなっているものと考えられます。

図5から加熱量の標準偏差も各回転角中、最も小さい値となっており加熱しやすくムラも少ないことが確認できます。 しかし、回転を考慮して時間的な平均を求めた点線と比較した場合、加熱量では回転角22.5°、337.5°の場合が大きいものの、加熱量の標準偏差はスターラーの回転を考慮した方が小さく、均一加熱に近づいています。

このことから、このケースではスターラーは加熱効率を犠牲にして加熱の均一性を図っているものといえます。

まとめ

今回の解析から次の結果が得られました。

• 回転するスターラーの加熱効率・均一性に対する影響を定量化する方法を提案し実際の解析で定量化しました
• スターラーは電子レンジにおいては加熱効率と均一加熱のトレードオフを図るデバイスであることが確認できました
• 電子レンジは様々な形状の料理や容器を加熱するため特定の形状に対して最適に設計することが出来ません

従ってどのような料理・容器に対しても平均的な性能が得られるよう回転するスターラーの導入は、特に、均一加熱の点で効果的だと考えられます。