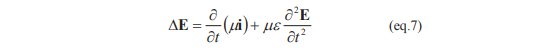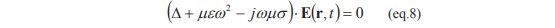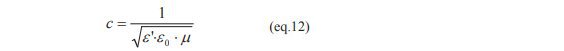マイクロ波加熱

物性変化を考慮した冷凍食品の電子レンジによる解凍シミュレーション

Electromagnetic Wave Analysis 3

～Microwave Heating～

Simulation of Thawing Frozen Food with a Microwave Oven Which Takes Variation of Physical Properties into Consideration.

Science and Technology Research Inst. Co.

要旨

マイクロ波が電子レンジ内部で加熱対象に入射する時、物性値や対象形状、レンジ庫内形状によって加熱量は一定ではなく分布します。特に冷凍食品のように温度による物性変化が大きいものは均一加熱が困難です。

ここではマイクロ波加熱のポイントとなる複素誘電率や媒質中の波長短縮、侵入深さなどの基礎知識を紹介します。

さらに電磁波解析ソフトウェアKeyFDTDを用いてマイクロ波により冷凍食品を加熱した場合の加熱量を定量的に予測しました。今回は冷凍ピラフを加熱対象とし、その解析結果を紹介します。またFDTD法による電磁波解析を用いた加熱量定量化の有効性を示します。

Abstruct

When microwave is incident on an object, quantity of heat distributes heterogeneously because of its physical properties or shape. Especially objects whose properties varies largely according to temperature like frozen foods are difficult to heat homogeneously.

In this chapter complex permittivity, shorter wavelength in media and penetration depth as the point of microwave heating with an electrical oven.

We simulated distribution of quantity of heat in frozen food placed in microwave oven quantitatively with electromagnetic analysis software, KeyFDTD. In this chapter we will focus on frozen pilaf as a heating target and will show the result. And we clarify that quantitation of distribution of heat with electromagnetic analysis using FDTD method is valid.

Maxwell 方程式と複素誘電率

誘電率 ε’の意味合いは捉え方によって様々ですが、マイクロ波加熱を考える場合には「マイクロ波のエネルギーを圧縮し溜め込める度合い」と理解するのが良いと思います。つまり同じ電界強度が誘電体中に存在する場合、誘電率の高い物質は低い物質に比べて、より多くのエネルギーを溜め込むことが出来ます。

なお注意するべき点は一般に誘電率と呼んでいる値は真空の誘電率 ε0 に対する比で本来「比誘電率」と呼ぶべき値ですが、「誘電率」という呼び方で一般的に呼ばれます。

誘電率 ε0・ε’を実部に持ち、虚部 ε0・ε’’で電磁波のエネルギーの吸収度合いを表したのが複素誘電率 εc です。つまり電磁波によって温まりやすい物質の複素誘電率虚部は大きく、温まりにくい物質では小さくなります。

複素誘電率の厳密な意味を考えるには Maxwell 方程式(eq.1～4)から考えると非常にわかりやすいです。

ここで、一様な誘電体中の電荷密度は波長スケールの空間を考慮する場合には一定と考えられるので(eq.6)の左辺第一項は 0 とおけます。また電流 i について i=σ・E の関係を代入すると次の(eq.7)が得られます。

この方程式の解として E(r,t)=E(r)exp(-jωt)を仮定し(eq.7)に代入すると次の（eq.8）となります。

ここで以下の(eq.9)で定義される εc を導入し、（eq.8）を書き直すと(eq.10)が得られます。

(eq.10)は電流による損失を考慮しない場合の波動方程式と全く同じ形です。複素誘電率の導入によって方程式の形を変えることなく損失を含む電磁波を扱うことが出来ることが表されました。

上記の εc は[F/m]の単位を持つ物性値ですが、多くの場合は真空の誘電率 ε0(=8.854187817…×10-12[F/m])との比である(eq.11)で表される ε’と ε’’をそれぞれ「誘電率」、「誘電損率」と呼びます。

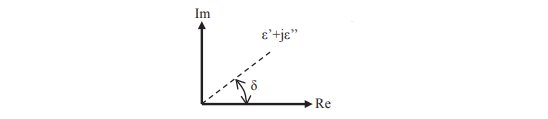
この二つを用いて ε’’/ε’で表される値は tanδ（タンジェントデルタまたは誘電正接）と呼ばれます。こう呼ばれる理由は上図に示すように、複素平面において実部に ε’、 虚部に ε’’を当てはめると、この比は ε’+jε’’と実軸がなす角度 δ の正接（tan）となるためです。

tanδ はマイクロ波加熱の分野では物質をマイクロ波で加熱した際の温まりやすさの指標として用いられます。つまり tanδ が大きな物質はマイクロ波で温まりやすく、小さな物質は温まりにくいと判断されます。電子レンジで用いられている周波数 f=2450[MHz]帯で水がtanδ=0.1 程度の値を持つため、食品を加熱することが出来ます。

余談ですが、コンデンサでは tanδ はエネルギーの圧縮率と損失の比となるため、小さい値の材料を如何に見つけて製造するかが重要になります。

波長短縮

電磁波の伝搬速度は約 3.0×108[m/s]です。但しこの値は真空中の値で、誘電体を伝搬する場合には小さい値になります。誘電体が空気のような気体の場合にはほとんど変化ありませんが、液体または固体に入射する場合には大きく変化します。

この時、電磁波の角周波数は変化しませんから、結果として電磁波の波長が変化します。真空中の光速より早く媒質中で電磁波が伝搬することはあり得ないので、媒質中では必ず光速は真空中よりも遅くなります。

(eq.10)であらわされる波動の伝搬速度 c は次の(eq.12)で与えられます。従って誘電体中の光速は誘電率 ε’の 2 乗根に反比例することが分かります。

例えば ε’=4 の誘電体に電磁波が入射した場合、電界（橙色）、エネルギー（赤色）は次の図 1 のように変化します。まず(eq.12)の関係から光速が誘電体内部では 1/2 になり、波長も同時に短縮して1/ (ε’)1/2 になります。

一方で波が持つエネルギーは 1 / 2・ε’・ ε0・ω・|E|2 で表され、真空中でも誘電体に入射した後も変化しないため電界の値は 1/2 に 低下します。

更に電磁波の一つの波に含まれるエネルギーは等しいので波長が短くなった結果として空間におけるエネルギー密度は 2 倍になります。

侵入深さ

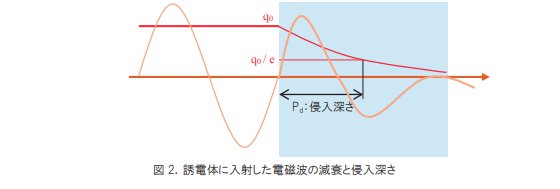
マイクロ波が誘電体に入射した時、そのエネルギーが熱として誘電体に奪われていきます。つまりマイクロ波は誘電体中で徐々に減衰しながら内部を進みます。エネルギーq0 を持った波が誘電体に入射する様子を模式化したのが図 2 です。

このような状況で入射した電磁波のエネルギーが 1 / e（約 37%）まで減衰する深さを侵入深さと呼びます。侵入深さ Pdは ε’と ε’’を用いて次の(eq.13)で求められます。

(eq.13)において分子は誘電体内部における波長を表しています。ε’’が大きいほど、電磁波のエネルギーは早く誘電体に熱として吸収されるため侵入深さは短くなります。

電子レンジによる食品加熱では ε’’が大きくなると加熱対象表面ばかりが加熱され、内部に電磁波が届かない状態になります。つまり均一に加熱することが難しくなります。この意味で食品の物性を代表する水の ε’’は程よい大きさの為、ほどほどに均一に温められます。

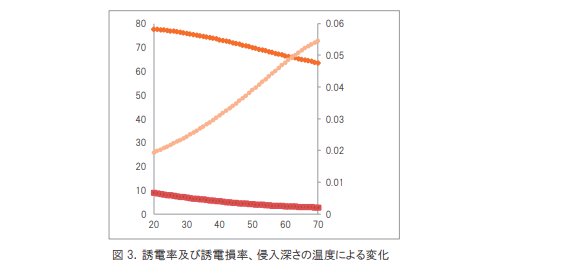
但し多くの物質で同じ周波数の電磁波に対しても温度が変化すると ε’及び ε’’は変化します。水の場合は双方ともに温度が高くなるにつれて小さくなりますが ε’’の方が割合としてより小さくなります。従って侵入深さは温度が上がるにつれて、より長くなります。

数値解析

冷凍ピラフを対象に、盛り形状の違いによる加熱量分布の違いを予測しました。更にある程度、解凍の進行により物性値が変化した場合の加熱量分布を予測しました。定量化を行いました。解析には、かぎけんが開発した電磁波解析ソフトウェア KeyFDTD を使用しました。

解析モデル

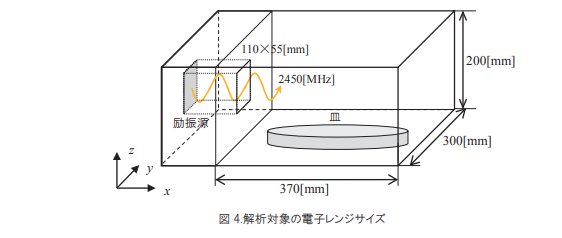
解析対象は、370×300×200[mm]の庫内容量を持つ家庭用電子レンジとします（図.4）。励振源は、側面から 110×55[mm]のアンテナで周波数 2450[MHz]のマイクロ波が TE10 モードで導入されるものとしました。庫内に皿(直径 250[mm]，厚さ 10[mm])が置かれその上に冷凍ピラフ(1 人前 250[g])を配置します。

冷凍ピラフ

冷凍ピラフは、前章「電子レンジ解凍のヒミツ」の米粒周囲を油が覆っているものと仮定します。ここで 1 粒 1 粒を再現するのは困難なので、冷凍ピラフを一様な物質とみなして物性値を与えました。

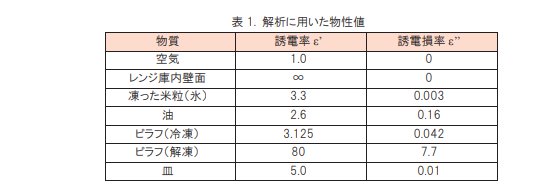
具体的には、氷と油の体積比により決定します。前章のピラフモデルでは体積比で氷(凍結ご飯):油 ≒ 3:1 ですので冷凍ピラフの誘電率 εpilafは氷の誘電率 εice、油の誘電率 εoilを用いて次の(eq.14)で与えました。

一般的に販売されている冷凍ピラフにはしばしば「皿に平らに盛って加熱」と記載されています。今回の解析では、電子レンジで冷凍ピラフを温める際に「平らに」、「盛り上げて」盛る 2 つのケースについて温まり方の違いを検証します。

解析ではまず平皿に 2 種類の形状でピラフを盛った状態をモデル化します。2 種類の形状をそれぞれ薄い円筒及び阪急、電子レンジ内にマイクロ波を照射したときの加熱量分布をシミュレーションにより求めます。

次に解析結果を参照に加熱量が多い部分の物性を解凍したピラフの物性に変更し再度計算することで、加熱前半及び後半における加熱量分布をシミュレートします。

加熱量分布の均一性定量化

上記のシミュレーション結果を用いて加熱量分布の均一性評価を定量的に行います。定量化に用いる加熱量偏差 δL は加熱量平均L (eq.15)を用いて、(eq.16)で表されます。

ここで、Σ は冷凍ピラフオブジェクト領域全体の総和、v は局所コントロールボリュームの体積、L は電力損失です。つまり、δL が小さいほど加熱ムラが小さい（均一加熱されている）ことを表します。この式を用いて、前述の 2 通りの盛り方をした冷凍ピラフのマイクロ波による加熱量分布を求めます。

解析設定 1（解凍開始時のピラフ）

2 ケースの解析で、総メッシュ数 251×201×151（＝762M）の直交均一メッシュを用いて解析を行いました。KeyFDTD では加熱対象にメッシュを集中させて、総メッシュ数を減少させ解析を高速化することもできますが、今回の解析では収束性と精度を重視し、このように設定しました。

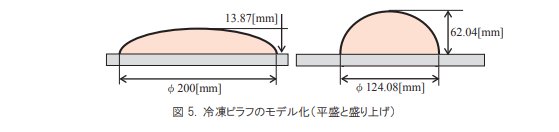
平盛りのケースは長径 100[mm]、短径 13.87[mm]の楕円回転体の上半分の形状で冷凍ピラフをモデル化しました。盛り上げるケースは半径 62.04[mm]の半球としました。この 2 ケースでピラフの体積は同じになるように設定しています。

物性値を表 1 に示します。

次の2つ図では、それぞれの盛り方で電子レンジ加熱した場合の加熱量シミュレーションの結果を示します。

解凍開始直後の解析結果

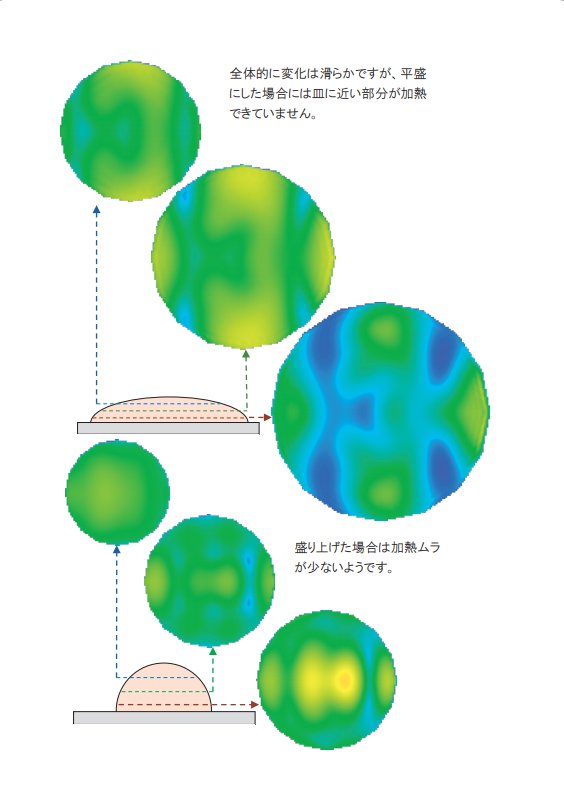
解析結果をみると、平盛りケースでは加熱庫内の電界強度分布がそのままピラフ内に侵入した分布になっています。一方、盛り上げたケースではピラフ中心に加熱量が集中しています。

平盛りの場合、ピラフの厚みが波長に比べて小さいため、強く入射した電磁波は強いままピラフを加熱すると考えられます。つまりピラフ自身の形状よりも、電子レンジの加熱庫内における定在波の分布が加熱量分布に大きく影響します。

一方で盛り上げた場合には厚みがピラフ内の波長よりも長く、かつ球形状のピラフ自身がレンズの働きをし、中心部に加熱量が集中するものと考えられます。つまり盛り上げた場合には加熱庫内の定在波の状況によらず中心付近で加熱量が大きくなるものと考えられます。

解凍が進んだ段階の解析モデル化とその結果

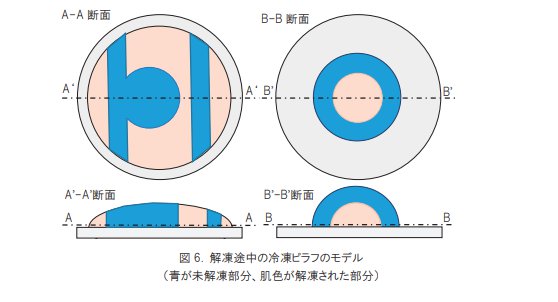
解凍が進んだ段階の解析モデルは解凍開始直後の解析結果を基に図 6 のように設定しました。解凍されたピラフ部分には、水（20℃）の物性値（ε=80-7.7j）を与えました。

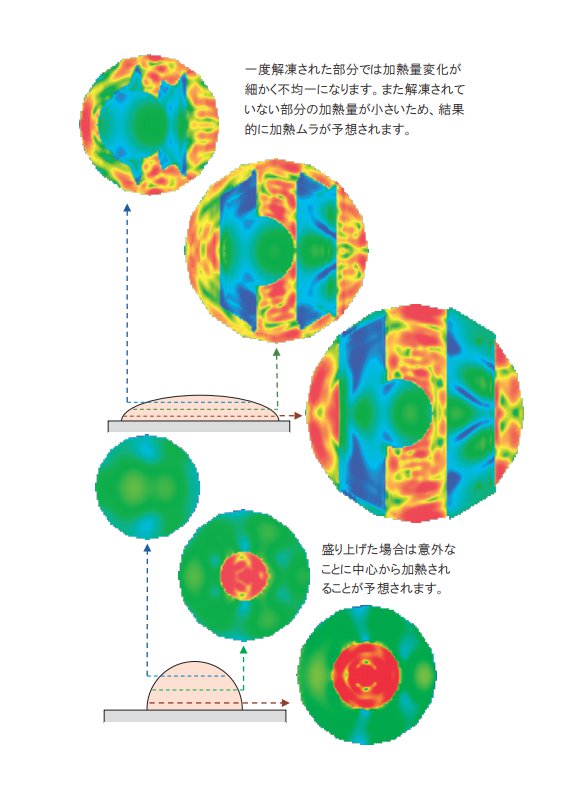
解凍が進んだ段階の解析では両ケース共に解凍箇所で極めて大きく加熱されています。本ケースでは電子レンジ庫内の定在波を時間的に撹拌するスターラーをモデル化していません。

このために平盛にしても盛り上げにしても加熱量の分布は不均一になりますが、平盛の場合であればスターラーが存在する場合には加熱量分布は平均化されます。スターラーが存在する場合の解析は科学技術研究書 2 に詳しいので省略しますが、スターラーの効果はシミュレーションでも確認されています。

盛り上げた場合には加熱量の集中が電子レンジ庫内の定在波分布によらず発生するためにスターラーを動作させたとしても加熱量分布は中心に集中することが予想されます。

加熱量分布の定量化

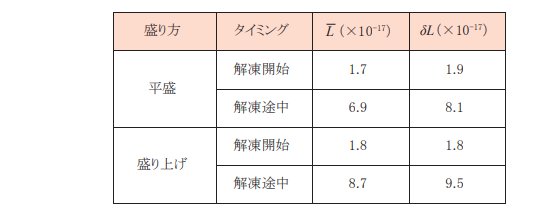
先述の解析に加えて、(eq.15)， (eq.16)で定義された加熱量標準偏差と平均加熱量を計算した結果は以下の通りです。

この結果より、解凍前は盛り方によらず同じような均一性で加熱されることが分かります。解凍後は盛り上げた方が平らにピラフを盛った時に比べ、加熱量が多く同時に加熱ムラも大きいことが予想されました。多くの冷凍ピラフで平盛が推奨されているのは電子レンジ加熱の効果よりも平盛にする段階で少し溶けた状態になることを利用して均一加熱に近づけているものと考えられます。